ضرب المصفوفات

إن عملية ضرب المصفوفات تختلف عن عملية ضرب الأعداد او حتى عن عمليات جمع وطرح وضرب المصفوفة بعدد حقيقي.

 فعملية ضرب المصفوفات تعتمد على رتبة المصفوفات اعتماداً كليا، فمثلا عند ضرب مصفوفتين يجب ان يكون عدد اعمدة المصفوفة الأولى مساوياً لعدد صفوف المصفوفة الثانية.

 وبالرموز إذا كانت ا مصفوفة من الرتبة  م × ن   والمصفوفة ب من الرتبة ن × ل فيمكن إجراء عملية الضرب حيث  أ م×ن  ×  ب ن×ل    ممكن  لأن عدد اعمدة المصفوفة أ مساويا  لعدد صفوف المصفوفة ب ، وتكون المصفوفة الناتجة من الرتبة م× ل .

تعريف :-

 إذا كانت أ مصفوفة من الرتبة  م× ن ،  ب  مصفوفة من الرتبة  ن× ل  فإن حاصل الضرب أ ب هو مصفوفةﺠ  من الرتبة  م × ل  بحيث

 ﺠ _{ي ﻫ} = أ _ي1 ب _{1 ﻫ}  + أ _ي2 ب2 _ﻫ + أ _ي3 ب_{3 ﻫ} + ........ + أ _{ي ن} ب _{ن ﻫ}  .

 مثال (6):

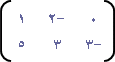، ب =

إذا كانت  أ =

أوجد (إن امكن ) كلاً من : أ ب ، ب أ .

الحل:-

أ  من الرتبة  2×2 ، 

ب من الرتبة  2×3  

 إذن  حاصل الضرب  أ ب  معرف ، لأن عدد أعمدة أ = عدد صفوف ب .

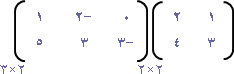أ ب =

=

ب أ : حاصل الضرب  ب أ غير معرف لأن عدد أعمدة  ب لايساوي عدد صفوف أ 

مثال (7): 

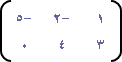، ب =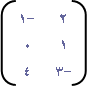

إذا كانت  أ =

فأوجد (إن امكن ) كلاً من :  أ ب ، ب أ  . ماذا تستنتج؟

 الحل:

أ من الرتبة 3 × 2 ،

ب من الرتبة 2 × 3 

إذن حاصل الضرب أ ب معرف، وكذلك حاصل الضرب ب أ معرف.

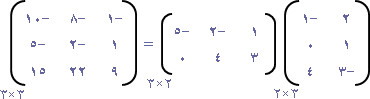أ ب =

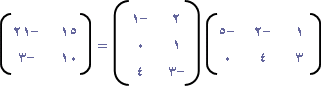ب أ =

نلاحظ أن أ ب  ¹ ب أ  أي عملية ضرب المصفوفات غير تبديلية . 

فيديو ضرب المصفوفات